Maturity is a concept that has existed since the 1950s. Since then, various equations have been proposed to measure the maturity of concrete. This chapter discusses three different methods that can be used in concrete maturity measurement: the temperature-time factor, the equivalent age, and the weighted maturity. All of the maturity methods are primarily dependent on the temperature history of the concrete but additional parameters related to concrete properties are also required to predict the in-place strength.

Temperature-Time Factor
The temperature-time factor (TTF) method, also known as the Nurse-Saul maturity function, was the first maturity method developed in the early 1950s, thanks to the work of Nurse[40] , McIntosh[36] and Saul[42]. The goal of their work was to understand the effect of accelerated curing and the impact of different curing temperatures on the strength development of concrete. This method was standardized in 1987 by ASTM C1074. Today, the Nurse-Saul function is the most commonly used maturity method in North America because of its simplicity.
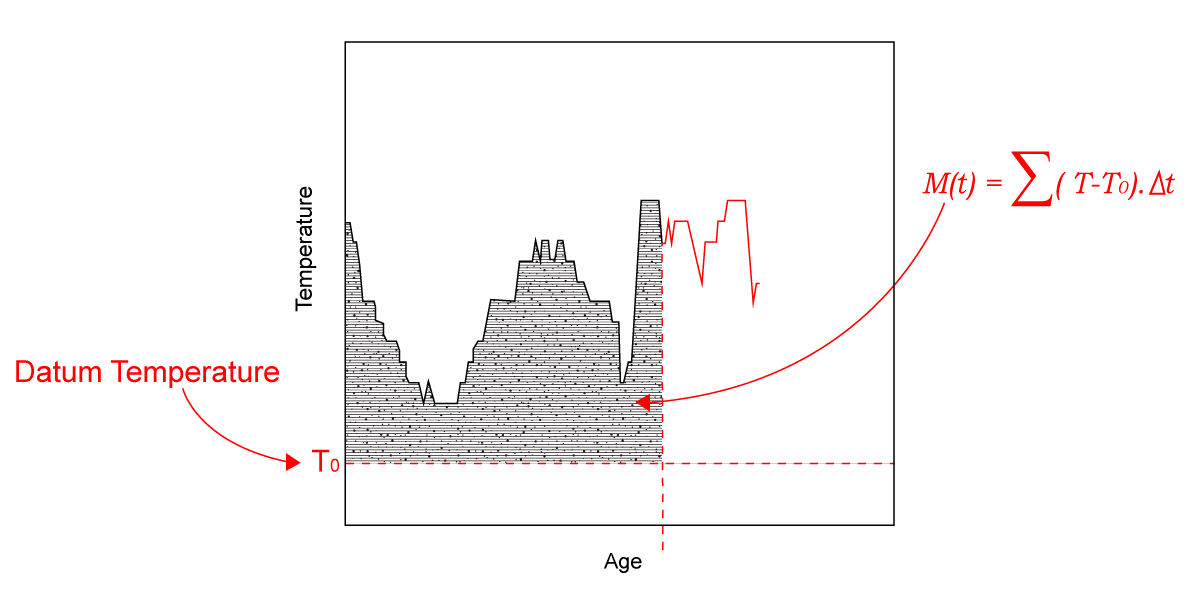
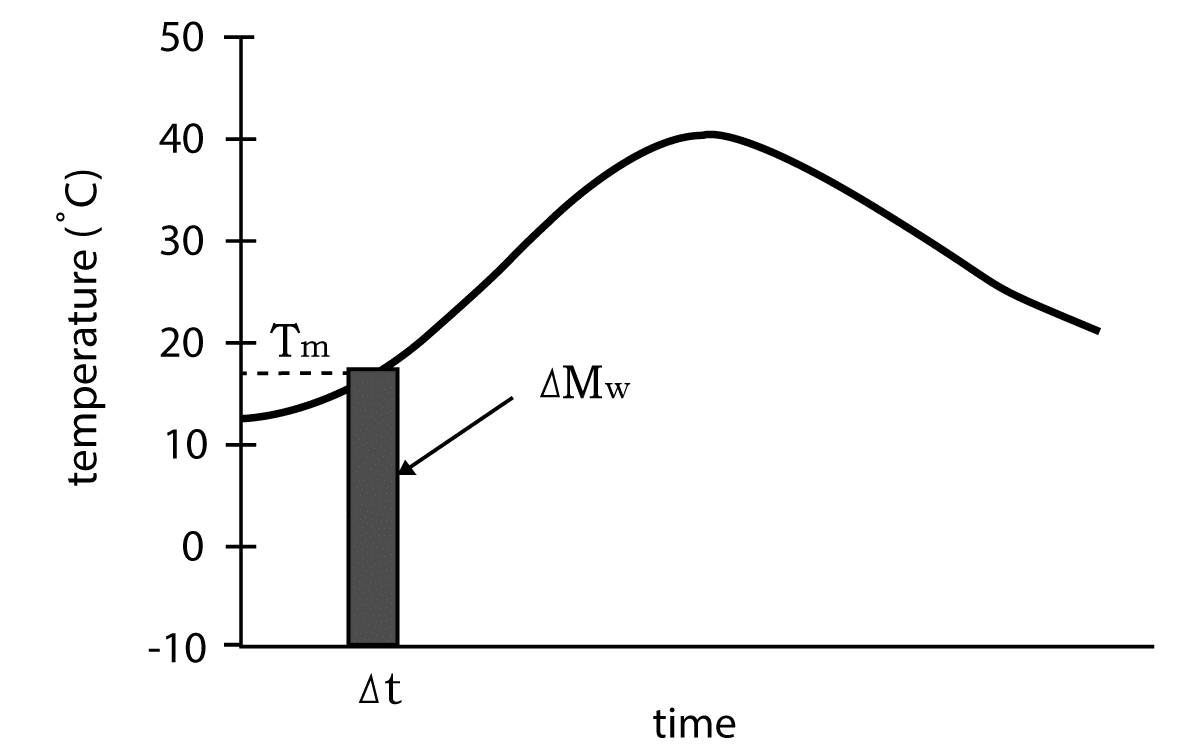
This approach takes into consideration that the maturity value is linearly dependent on temperature and can simply be represented by the area below the temperature curve, as graphically shown in Figure 4-1. In this approach, the area under the temperature curve is taken as the difference between the average recorded temperature and the datum temperature (T). The datum temperature is defined as the temperature at which the hydration of the cement stops, in other words, the temperature at which concrete stops developing strength. The Nurse- Saul equation is mathematically represented as follow:

Most of the variables in Eq. 4-1 can easily be obtained without a complex analysis. “T” is simply obtained by the maturity monitoring system at a given time. “?t” is the default value given by the frequency of measurements taken by the maturity meter and is usually defined as 1 hour, 30 min, or less. The only variable that is unknown and needs to be calculated or estimated is the datum temperature. For a better accuracy, “T” can be calculated through laboratory testing as specified in ASTM C1074, but, in most cases, it can be defined as 0ºC (32ºF), -5ºC (23ºF) or -10ºC (14ºF).
ASTM C1074 states that: “for type I cement without admixture and a curing range between 0 to 40ºC, the recommended datum temperature is 0ºC”. Originally, the datum temperature was defined as -10ºC. However, studies have shown that the datum temperature for any given type of cement is within 0 to -10ºC. Assuming a 0ºC datum temperature in most cases is often considered a conservative approach, as it assumes that there is no strength gain if the temperature of the concrete falls below freezing point. Since concrete cannot lose strength as it hydrates, any given condition that would cause (Ta – Td) ? 0 would result in no strength gain, M(t) = 0.
During the summer, when the temperature of the concrete is higher, assuming any datum temperature from 0 to -10ºC for calibration will not necessarily have a significant impact on the results. However, in winter when the temperature can easily fall below freezing in certain regions, closer attention needs to be given when determining the actual datum temperature. In general, project specifications require that the temperature of the concrete remain above a certain temperature (>5ºC) for a certain period of time during curing.
Example
Figure 4-2 and Figure 4-3 below show an example of maturity and strength calculations using different datum temperature (0ºC, -5ºC, -10ºC). Each maturity calibration curve was developed by taking into account the different datum temperature to calculate maturity for the same strength data. The difference of those three mix calibrations are shown in Figure 4-2, where it is possible to observe that any difference is simply a shift to the right because the maturity corresponding to each strength gets larger as the datum temperature decreases (more area under the temperature curve). Given a temperature curve that falls below freezing point, it is possible to observe how the maturity and strength value can vary for different datum temperatures (Figure 4-3).
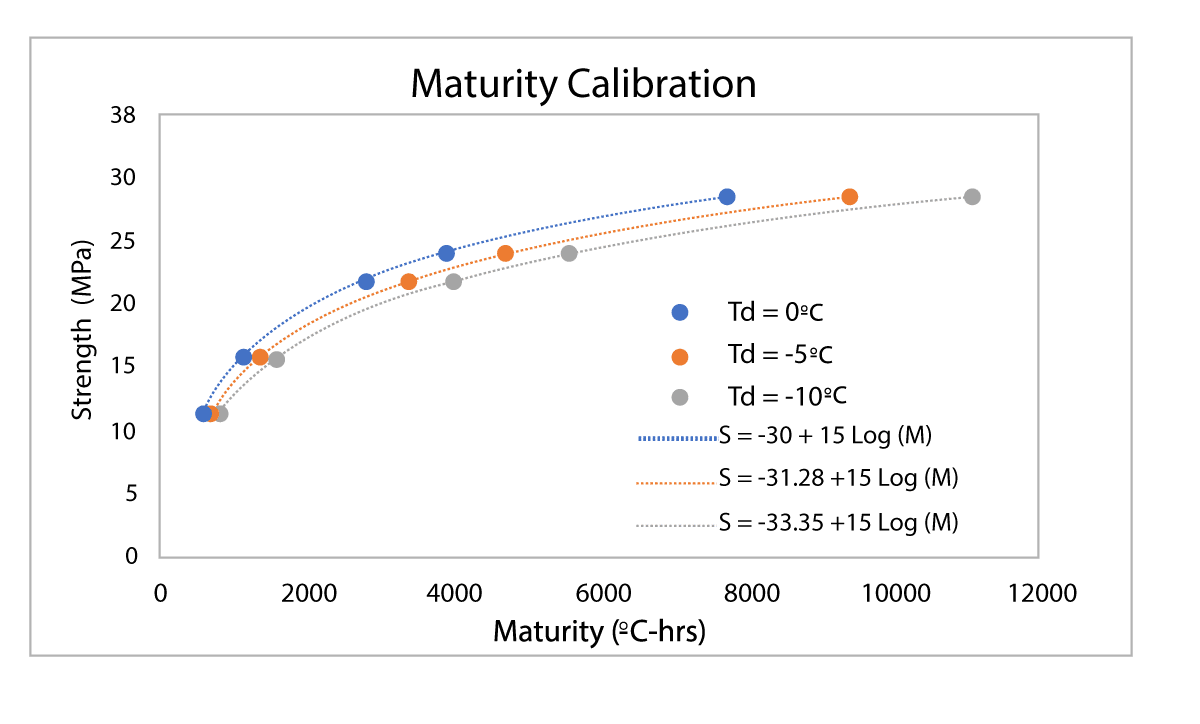
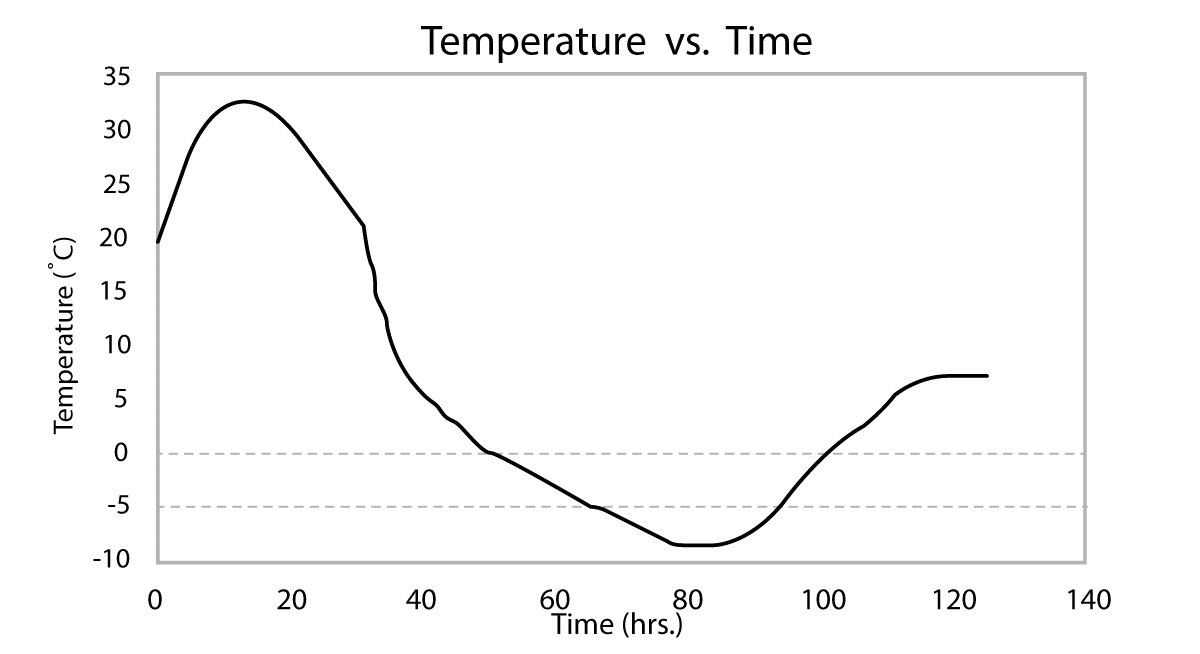
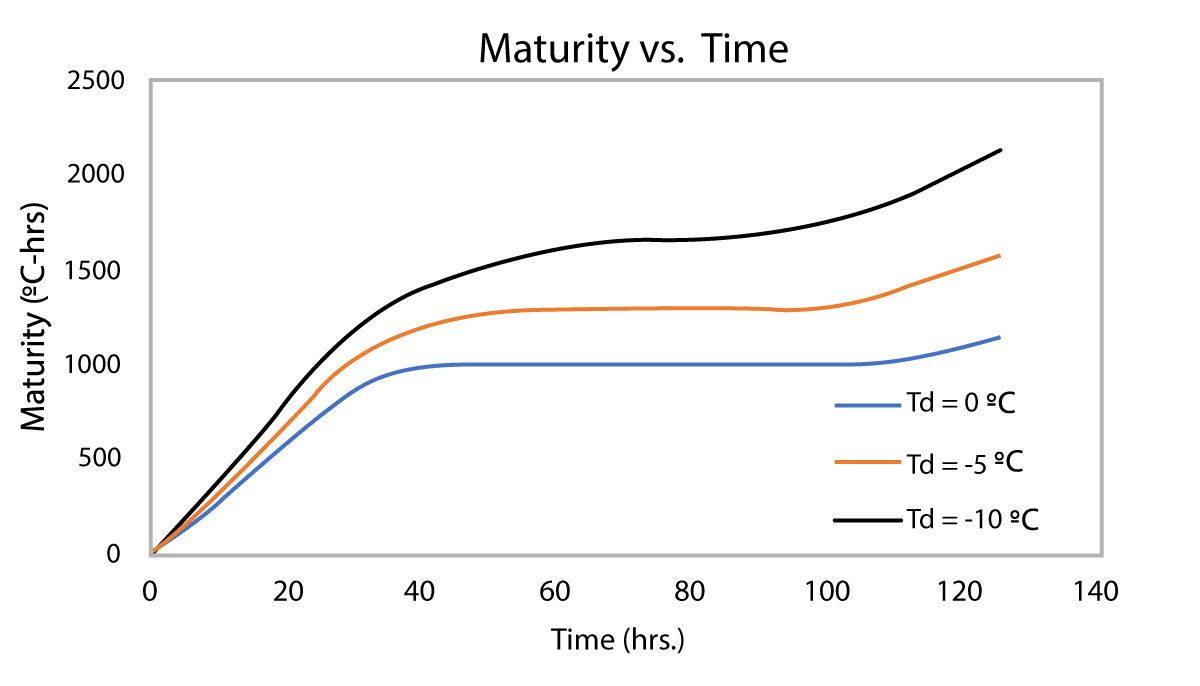
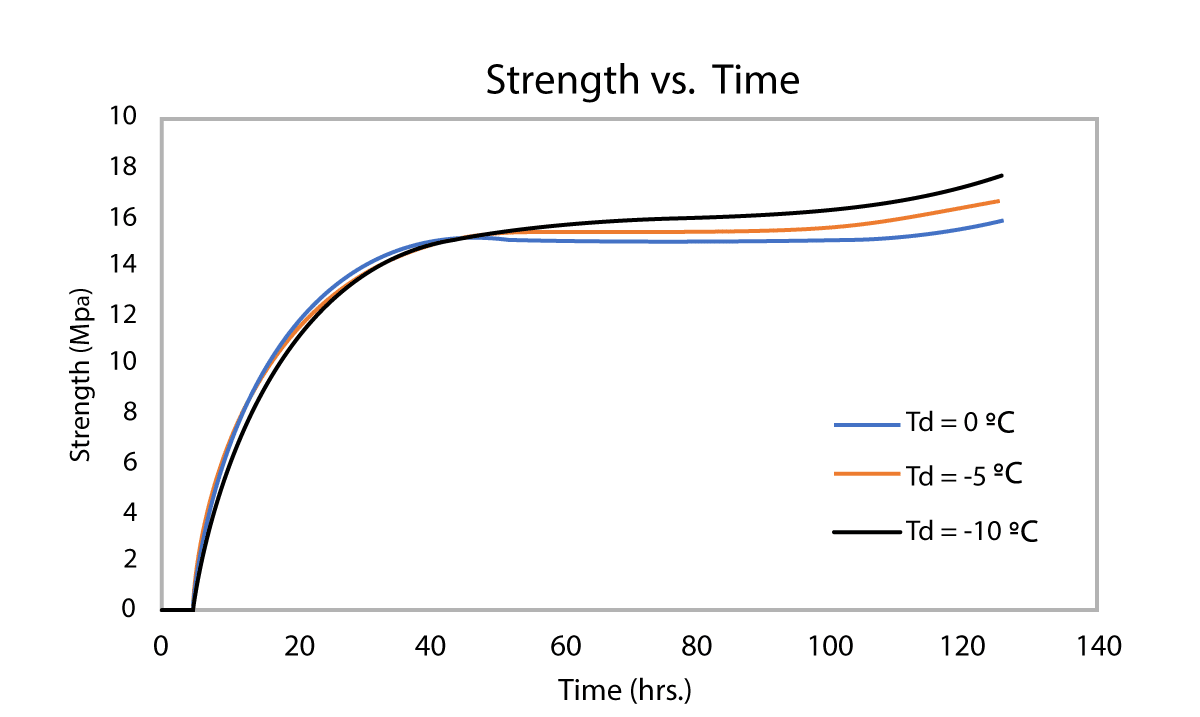
Figure 4-3: Effect of datum temperature on the maturity and strength calculations
4.1.1. Datum Temperature Calculation
As mentioned above, “Ta” can be defined as 0ºC for simplicity (other temperatures also used in the industry are -5ºC and -10ºC). Nevertheless, it is possible to determine the datum temperature by following the steps provided in ASTM C1074 A1, which are summarized below.
The datum temperature procedure consists of making a minimum of 54 mortar cubes (ASTM C109) representing the concrete mix. The cubes should be divided into 3 different sets; each containing 18 cubes. Each of these three sets will be cured at a different temperature. The temperature chosen for curing should be based on the maximum and minimum expected curing temperature as well as an average temperature of the jobsite. Three cubes are then broken at six different times to obtain the strength of the concrete (ASTM C109).
4.1.1.1. Rate Constant (K-value)
To calculate the datum temperature, the k-value must be determined for each curing condition. The k-value is the reaction rate constant which is dependent on time and temperature. It represents the rate of the chemical reaction, in this case, the cement hydration reaction which represents the strength development in concrete.
There were originally 3 approaches suggested by ASTM C1074 to determine the k-value, in the last revision of ASTM C1074 only one approach was kept as the standard procedure to determine the reaction rate k.
The k-values can be solved using a computer program for Eq. 4-2. In this equation, in addition to the rate constant, “to” and “Su” are also unknowns that need to be solved, ASTM C1074- 17 provides an example of calculation and spreadsheet set up to solve for those parameters.
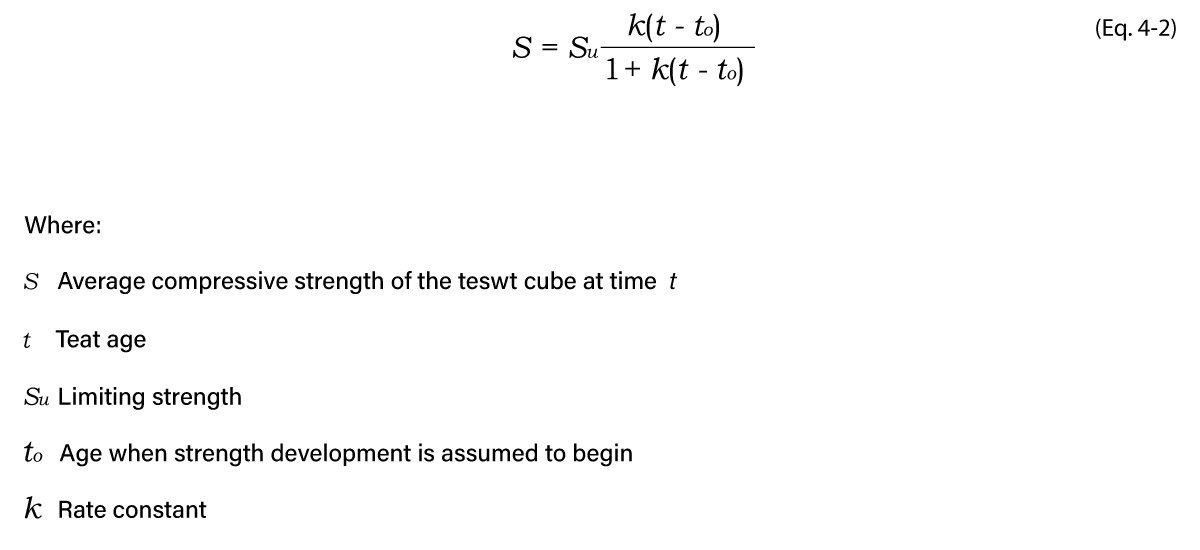
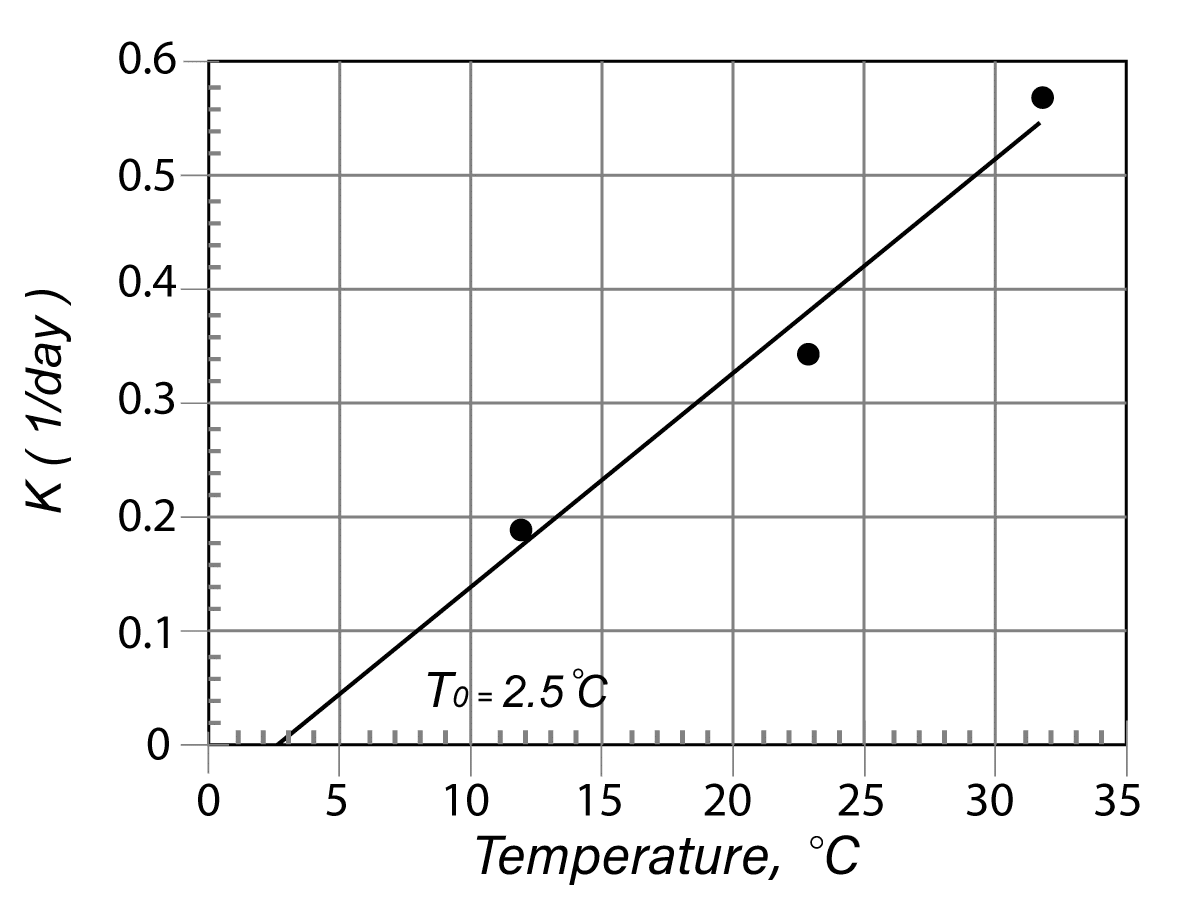
Once the k-value has been calculated for each curing temperature, the reciprocal of k vs. curing temperature can be plotted. By fitting a linear interpolation, the intersection with the x-axis represents the datum temperature (Figure 4-4).
4.2. Equivalent Age
Even though the temperature-time factor equation is widely used and accepted worldwide, the linear approach to determine maturity is not accurate for all curing conditions, especially at temperatures outside the range of 0-40ºC. To mitigate this effect, in 1977 Freiesleben-Hansen and Pedersen proposed a more accurate equation in which the maturity is exponentially dependent on temperature. This maturity method is known as the equivalent age method and is based on the Arrhenius equation. This approach is standardized in most codes including ASTM C1074 and European standards (European countries typically allow the Arrhenius method instead of the Nurse-Saul). Despite the fact that this approach is a bit more complex than the temperature-time factor, if the assumptions are done properly, it can lead to a more accurate prediction of the in-place strength. The equivalent age can be calculated using Eq. 4-3.
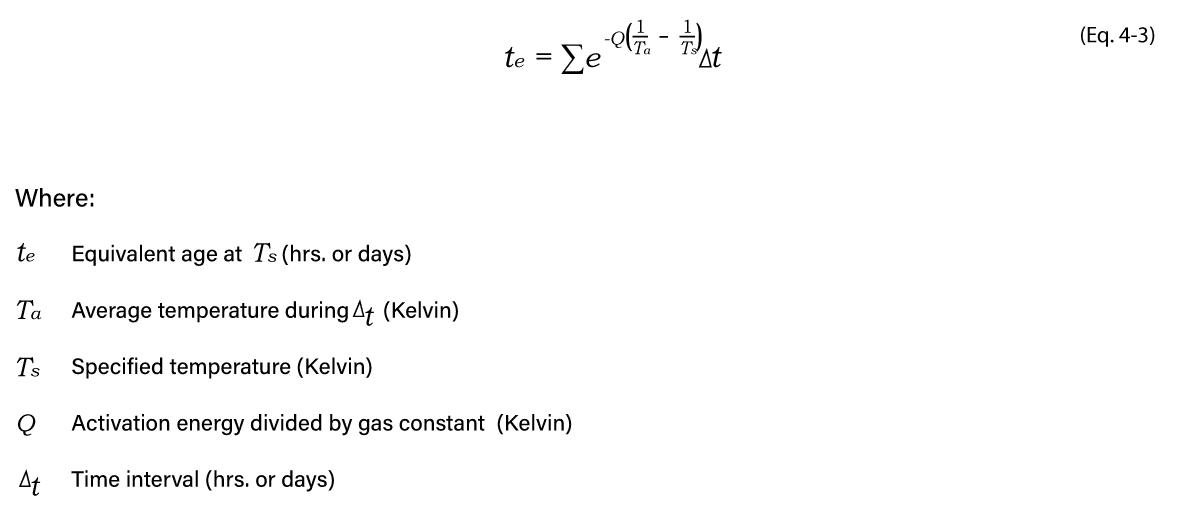
Similar to the Nurse-Saul equation, “Ts” and “?t” can be obtained from the maturity meter. “Ts” represents a specified temperature and is usually defined as 23ºC in North America and 20ºC in Europe. The activation energy divided by gas constant must be determined experimentally using very similar steps as shown in the calculation of datum temperature. ASTM C1074 also proposes a standard value where Q can be defined as 5000 K for type I cement without admixtures.
To determine “Q”, the k-value must be obtained following the same steps presented in Section 4.1.1.1. By plotting the natural logarithm of k vs. the reciprocal of the curing temperature (in Kelvin), the negative of the linear slope represents “Q”.
4.3 Weighted Maturity
The third method proposed to calculate maturity is the weighted maturity, which was developed in the 1970s by Papadakis and Bresson and later modified by de Vree in 1979. This method is not typically used in North America as it is not standardized by ASTM C1074. However, it is currently standardized in the Netherlands (NEN5790) and accepted in Europe.
The general approach of the weighted maturity method is described in Eq. 4-4. This equation is very similar to the Nurse-Saul equation as “tkTk” represents the area under the temperature curve while the “Cnk” represents a correction factor.

Using this equation is, however, not practical as the “nk” factor is temperature-dependent. A discontinuous function to simplify the calculation of the proposed linear equation (Eq. 4-5), can be used in determining the n parameter. Therefore, the weighted maturity equation can be rewritten in a simpler form by taking the integral of “Cnk” from datum temperature (-10ºC) to average temperature. The weighted maturity equation can now be defined as Eq. 4-6 with a continuous n function. It is graphically represented in Figure 4-5.
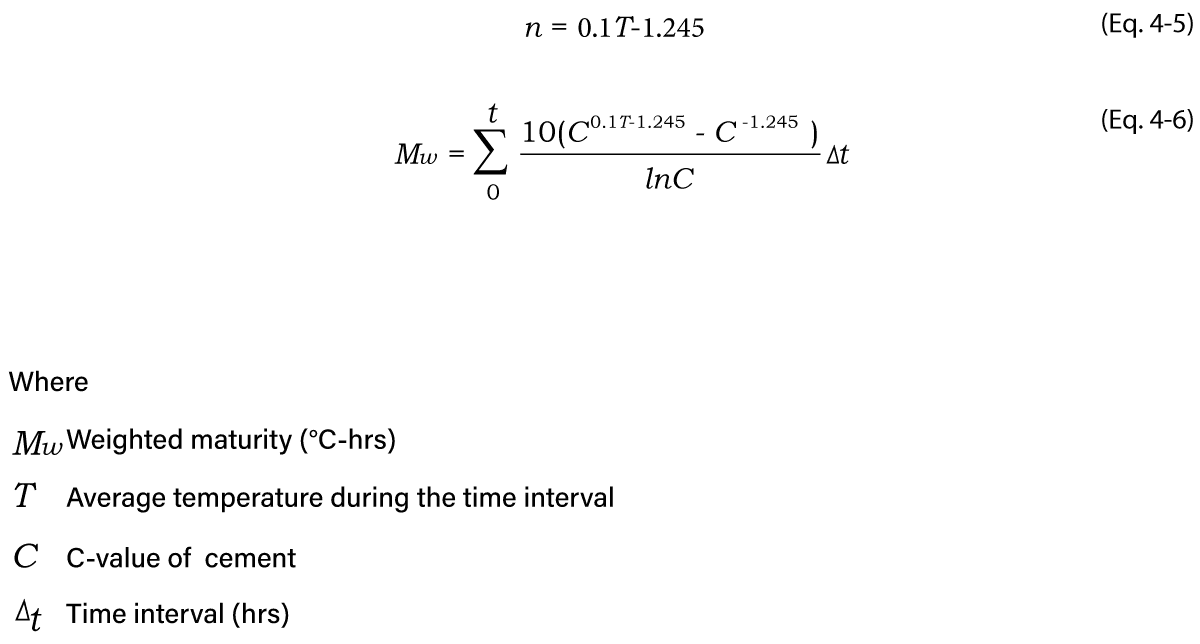
The C-value is a cement-specific value which indicates the influence of the sensitivity of the cement to temperature. The C-value can be obtained directly from the cement producer or through the standardized procedure in NEN 5790. The value typically varies from 1.25 to 1.75.
**Editor’s Note: This post was originally published On July 19, 2019 and has been updated for accuracy and comprehensiveness.











2 Responses
Concrete monitoring system from production till completion including maturity calculator, temperature monitoring, strength monitoring, surface finish monitoring, uniform color monitoring with the integration of software tools is required
Hi,
In one of our project we follow this specification, can u guide me what is the equipements required to fullfill the needs.
Hi Ilango, thank you for your comment. To monitor concrete maturity on your jobsite all you need is a concrete maturity sensor, like SmartRock. Once installed on the rebar, it gives you strength/maturity on your mobile device. No other equipment is needed except for the sensors and your phone. Read more about SmartRock here https://www.giatecscientific.com/products/concrete-sensors/smartrock-maturity-meter/